Merkle Trees....continued (#4)
Today we'll be implementing Merkle Trees. This is building upon the last post.
Hey folks, we’re back for another post. Today, as promised in the previous post, we’ll be implementing Merkle Trees. I will do my best to provide the implementation in multiple languages.
Note: I’m currently trying to get better at Golang so I’ll be implementing the tree in that.
Shout-outs
We’ve gone from 48 subscribers last week to 57 this week. I’m beyond grateful for all the subscribers. Hopefully you all are enjoying the content. I’ve gotten a few requests from subscribers and I’d like to see what folks want to see more of:
Recap
Let’s quickly recap what we discussed last time. We talked about the tree data structure and how it represents a hierarchy consisting of nodes classified as root, children, and leaf. We then went on to define and discuss a special type of tree, a Merkle tree.
We defined a Merkle tree as a binary tree in which every leaf node contains the cryptographic hash of a data element while every non-leaf node contains the cryptographic hash of the sum of cryptographic hashes of its children. Below is our definition in a visual format:
Implementation
Let’s get started implementing the Merkle Tree. We’ll start by defining our high level data structures:
MerkleNode: this will represent a singular node. As we’ve outlined a node can have a left child and a right child. Secondly, a node either contains the hash of a data element or the hash of the concatenation of its childrens hashes.
MerkleTree: the tree itself is represented by the root node, the MerkleRoot
// Let's define a Node N
// A node can have a left child and a right child
// A node also contains the cryptographic hash
type MerkleNode struct {
LeftChild *MerkleNode
RightChild *MerkleNode
Hash string
}
type Tree struct {
MerkleRoot *MerkleNode
}Above we've defined the MerkleNode which contains the members LeftChild, RightChild and Data. We've also defined the Tree itself. The Tree struct only has one member...the MerkleRoot.
With our data structures set up let’s now tackle actually creating a node. As stated above, a node can have children and that determines what is hashed and stored.
func NewMerkleNode(leftChild, rightChild *MerkleNode, data []byte) *MerkleNode {
node := MerkleNode{}
if leftChild != nil && rightChild != nil {
oldHash := leftChild.Hash + rightChild.Hash
newHash := sha256.Sum256([]byte(oldHash))
node.Hash = hex.EncodeToString(newHash[:])
} else {
hash := sha256.Sum256(data)
node.Hash = hex.EncodeToString(hash[:])
}
node.LeftChild = leftChild
node.RightChild = rightChild
return &node
}Our function NewMerkleNode takes in three inputs; the left child, right child, and the data itself. We then create an empty MerkleNode and explicitly check if we passed in valid values for left and right child. If we did, we update the hash accordingly. We then return the memory address of the node.
To highlight how this would work, imagine if we wanted to create a brand new leaf node the way we would do that is:
leafNode := NewMerkleNode(nil, nil, []byte("data"))Similarly, if we wanted to create a regular node with left and right children it would look something like this (assuming the left and right children have already been created):
node := NewMerkleNode(leftChild, rightChild, []byte(""))Now that we’ve got a way to create nodes, we need a way to construct the tree itself. The gist of constructing a tree is you climb up the tree creating new levels until you reach the top, the root node.
As a thought exercise, let’s imaging we’re given a bunch of data blocks and we’re asked to construct the Merkle Tree, it would look something like this:
Create leaf node corresponding to each data block
Go up one level creating nodes corresponding to the lower level leaf nodes
Go up one level creating nodes corresponding to the lower level nodes
And so on….. until we’ve reached a singular node.
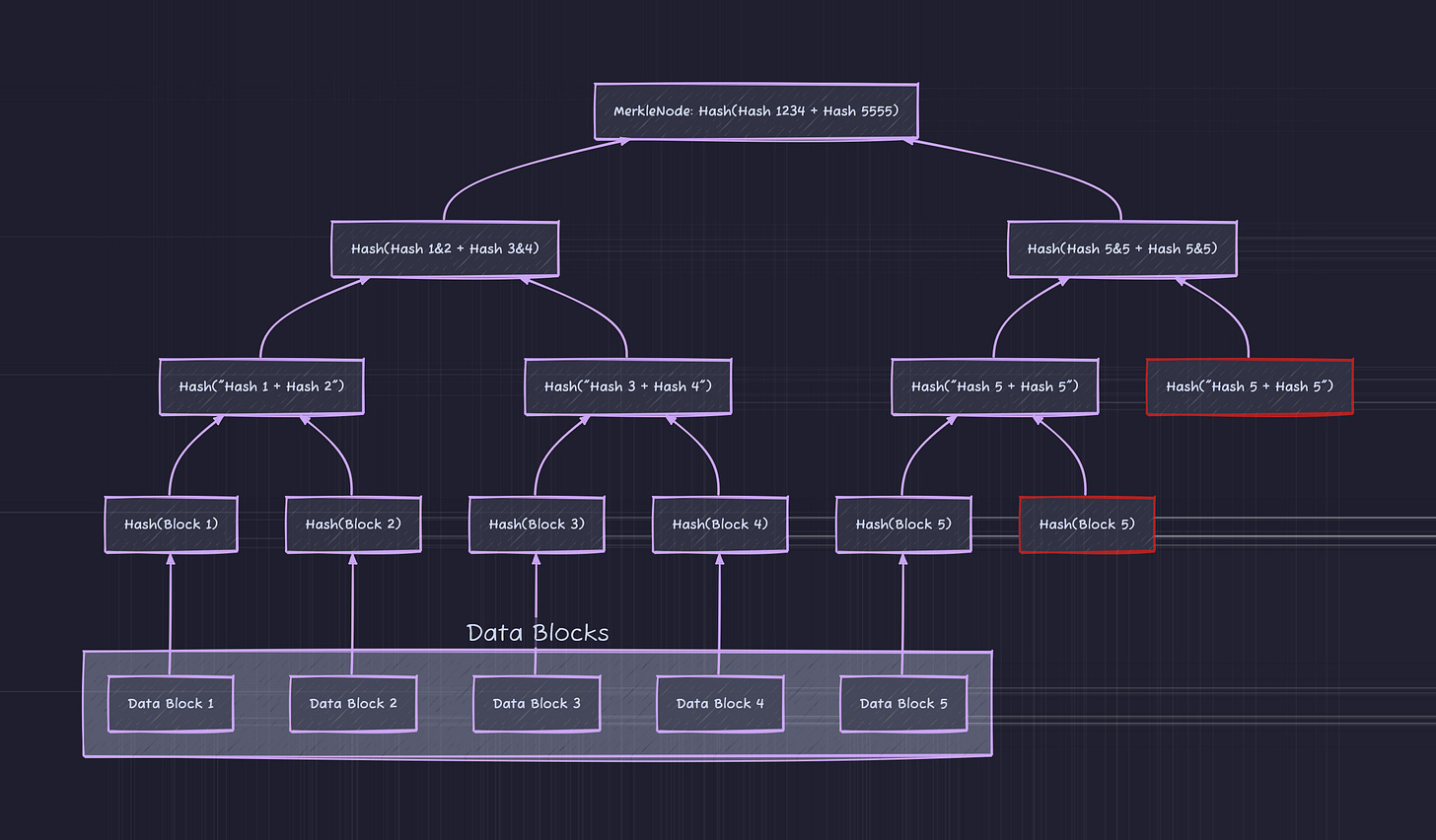
One thing we need to watch out for is an odd number of nodes at any level besides the root node. For example, lets visualize having 5 data blocks to encrypt:
As you can tell there are only 5 nodes, there aren’t an even number of nodes, so we append the last node again to make it look like this:
No we have an even number of nodes lets start moving up the chain.
Once again we find ourselves in a situation where we need to replicate the last node at this level (in this case Hash(“Data Block 5 + Data Block 5”)). As we replicate and move up this is what we end up with:
So as you can notice, we had to replicate two nodes (the ones in red, obviously). We have to take this into account when coming up with the logic to create the tree.
func NewMerkleTree(dataBlocks [][]byte) (*Tree, error) {
if len(dataBlocks) == 0 {
return nil, errors.New("must have more than 0 data blocks")
}
var nodes []MerkleNode
// Handle odd number of data blocks by replicating the last one.
if len(dataBlocks)%2 != 0 {
dataBlocks = append(dataBlocks, dataBlocks[len(dataBlocks)-1])
}
// Create leaf Nodes
for _, data := range dataBlocks {
nodes = append(nodes, *NewMerkleNode(nil, nil, data))
}
// Time to construct the tree level by level
for i := 0; i < len(dataBlocks)/2; i++ {
var newLevel []MerkleNode
for j := 0; j < len(nodes); j += 2 {
// If the number of nodes at the level are odd, once again append the last one at the end
if len(nodes)%2 != 0 {
nodes = append(nodes, nodes[len(nodes)-1])
}
newLevel = append(newLevel, *NewMerkleNode(&nodes[j], &nodes[j+1], nil))
}
nodes = newLevel
}
// return the tree
return &Tree{MerkleRoot: &nodes[0]}, nil
}To deal with the possibility of there being an odd number of nodes at any given level, there’s a check to make sure that we have an even number of nodes, if we don’t just append the last node to the array and carry on.
What this function does is:
Create leaf nodes from the input data.
Check if there’s an even number of data blocks, if not replicate the data block.
Create nodes level by level making sure to check if there are an even number of nodes every time.
Return the Tree struct with the MerkleRoot set to the only element in the nodes array.
Using this function would look something like this:
testData := [][]byte{
[]byte("Transaction 1"),
[]byte("Transaction 2"),
[]byte("Transaction 3"),
[]byte("Transaction 4"),
[]byte("Transaction 5"),
}
tree, err := NewMerkleTree(testData)Okay, we’ve implemented it but how can we check if it’s right? How can we verify that the hashes line up? With a simple breadth-first search (BFS) of the tree.
Let’s verify along the way:
Data Blocks
Data: Transaction 1 Hash:dff3b30655dc240deca00ed22fae68fdf8cf465bbe99bb2b2e24259cc1daac3a
Data: Transaction 2 Hash:4ae0e48b754a046b0f08e50e91708ddff4bac4daee30b786dbd67c30d8e00df8
Data: Transaction 3 Hash:2b8fd91deadf550d81682717104df059adc0addd006a0c7b99297e88769b30e5
Data: Transaction 4 Hash:b99ca09efe93055ad86acb5bfc964e16393d8e4672c3a4c5fa08ffabc85065b3
Data: Transaction 5 Hash:40d1474d042b66b26df83eae197368b93d84d8c960d39aec68573796078114a4
Data: Transaction 5 Hash:40d1474d042b66b26df83eae197368b93d84d8c960d39aec68573796078114a4You can see that Transaction 5 is repeated.
Level 0 (Immediately above Data Blocks)
Printing levels...
Level 0...
Hash Left: dff3b30655dc240deca00ed22fae68fdf8cf465bbe99bb2b2e24259cc1daac3a Hash Right: 4ae0e48b754a046b0f08e50e91708ddff4bac4daee30b786dbd67c30d8e00df8 New Hash: a31d3187c179a847bc0fbe729e06a0770147ad58b45995ac945032df15ba38e3
Hash Left: 2b8fd91deadf550d81682717104df059adc0addd006a0c7b99297e88769b30e5 Hash Right: b99ca09efe93055ad86acb5bfc964e16393d8e4672c3a4c5fa08ffabc85065b3 New Hash: c6dadc3fe8fde36887f07ed12e0bb073b4165d0921749b98b2ae237f3aed3e07
Hash Left: 40d1474d042b66b26df83eae197368b93d84d8c960d39aec68573796078114a4 < Hash Right: 40d1474d042b66b26df83eae197368b93d84d8c960d39aec68573796078114a4 < New Hash: 745ebfe140c7e62a45766934adff116dcd736890477b37ccd44550284d38e7c2You can see each of the data block hashes being used. And the < marks the replicated node.
Level 1
Level 1...
Hash Left: a31d3187c179a847bc0fbe729e06a0770147ad58b45995ac945032df15ba38e3 Hash Right: c6dadc3fe8fde36887f07ed12e0bb073b4165d0921749b98b2ae237f3aed3e07 New Hash:7e1182c5c00e379261503e757487cfa16cda7010f1ca3ae0115d5b78cfc07509
Hash Left: 745ebfe140c7e62a45766934adff116dcd736890477b37ccd44550284d38e7c2 < Hash Right: 745ebfe140c7e62a45766934adff116dcd736890477b37ccd44550284d38e7c2 < New Hash:c4a338ab87fe2e56055a48e160f007ebb6a8a90303659fd8b97dde9d99a9a164Same as before you can see where the node was replicated and you can see where the hashes from Level 0 are used here.
Level 2 (Merkle Root)
Level 2...
Hash Left: 7e1182c5c00e379261503e757487cfa16cda7010f1ca3ae0115d5b78cfc07509 Hash Right: c4a338ab87fe2e56055a48e160f007ebb6a8a90303659fd8b97dde9d99a9a164
New Hash: 2c2c4cdf817ca1233db4784bb8752eddca8428c5c88ad7fad7e7235532e33c3cAnd there we go, we’ve reached the top, the Merkle Root.
Verification
Now that we have a merkle tree, how can we verify an element of the original data block?
Scenario: you’re hosting a file on Dropbox and need to retrieve it. Dropbox partitions the file and stores the file in chunks across multiple nodes. When retrieving your file Dropbox will use a Merkle Proof to verify that a chunk belongs to the requested file.
So given data blocks and a specific data block to verify how can we ensure that the specific data block is part of the Merkle Tree? This is where a Merkle Proof comes in to play.
A Merkle Proof (defined as a Merkle Consistency Proof in RFC6962) is basically the list of nodes in the Merkle Tree required to verify that the input is contained in the tree.
Let’s visualize this:
Let’s say we want to verify that Data Block 1 (blue) is included in the Merkle Root Node for the tree, what nodes do we need to verify that?
We can generate the hash for Data Block 1
We need the hash for Data Block 2 (green)
We can now generate the hash for Hash (Hash 1 + Hash 2)
We need the hash for Hash (Hash 3 + Hash 4) (green)
We can now generate the hash for Hash (Hash 1&2 + Hash 3&4)
We need the hash for Hash (Hash 5&5 + Hash 5&5) (green)
We can now calculate the hash for the Merkle Root. Thus verifying Data Block 1’s inclusivity.
This means for Data Block 1 the Merkle Proof is:
[Hash(Block 2), Hash(Hash 3 + Hash 4), Hash(Hash 5&5 + Hash 5&5)]Implementation
Let’s implement the verification process. This will be two parts:
Build the proof:
Which hashes lead to the MerkleRoot
Verify the proof
Do the hashes hash their way to the Root
Build the Proof
Lets say we’re given an array of data blocks and a specific data block we want to verify. How do we approach this? This is almost entirely identical to building the actual Merkle tree, the only difference is that we’ll append the hashes we need to an array and return them.
func (tree *Tree) MerkleProof(data []byte, dataBlocks [][]byte) ([]string, error) {
// Find index of the data block we're looking for
// Determines whether we have a left or right sibling
index := -1
for i, block := range dataBlocks {
if bytes.Equal(data, block) {
index = i
break
}
}
if index == -1 {
return nil, errors.New("data not found in datablocks")
}
// Get the leaf hashes
var proof []string
var hashedNodes []*MerkleNode
for _, data := range dataBlocks {
hashedNodes = append(hashedNodes, NewMerkleNode(nil, nil, data))
}
// We will now construct the tree and traverse up to verify
// Basically build the tree and add the necessary nodes to our proof
for len(hashedNodes) > 1 {
var nextLevel []*MerkleNode
// If even we have a right sibling, if odd we have a left sibling
if index%2 == 0 && (index+1 < len(hashedNodes)) {
proof = append(proof, hashedNodes[index+1].Hash)
} else if index%2 == 1 {
proof = append(proof, hashedNodes[index-1].Hash)
}
for j := 0; j < len(hashedNodes); j += 2 {
if j+1 < len(hashedNodes) {
nextLevel = append(nextLevel, NewMerkleNode(hashedNodes[j], hashedNodes[j+1], nil))
} else {
nextLevel = append(nextLevel, NewMerkleNode(hashedNodes[j], hashedNodes[j], nil))
}
}
hashedNodes = nextLevel
index /= 2
}
return proof, nil
}This code will give us an array of hashes, that when used will re-construct our MerkleRoot.
Verify the Proof
This part is the easiest, we will quite literally just hash each member of the proof array until we reach the MerkleRoot.
To do this we’ll write two helper functions to make our lives easier:
leafHashwhich will hash the contents as if it were a leaf.nodeHashwhich will hash the contents as if it were two nodes.
func nodeHash(leftHash, rightHash string) string {
newHash := sha256.Sum256([]byte(leftHash + rightHash))
return hex.EncodeToString(newHash[:])
}
func leafHash(data []byte) string {
hash := sha256.Sum256(data)
return hex.EncodeToString(hash[:])
}With the helper functions in place, lets implement the verifier. We will return true if the data block is part of the Merkle Tree and false otherwise.
func VerifyMerkleProof(data []byte, proof []string, rootHash string) bool {
leaf := leafHash(data)
for _, siblingHash := range proof {
leaf = nodeHash(leaf, siblingHash)
}
return leaf == rootHash
}That’s it we’re done. Now to actually run through it we’ll reuse the data from above, lets check if Transaction 1 is in the Merkle Tree:
output, err := tree.MerkleProof([]byte("Transaction 1"), testData)When executed, output looks like this (a list of hashes that when hashed with the original data block should give us the MerkleRoot):
[4ae0e48b754a046b0f08e50e91708ddff4bac4daee30b786dbd67c30d8e00df8 c6dadc3fe8fde36887f07ed12e0bb073b4165d0921749b98b2ae237f3aed3e07 c4a338ab87fe2e56055a48e160f007ebb6a8a90303659fd8b97dde9d99a9a164]Now to verify the proof:
proof := VerifyMerkleProof([]byte("Transaction 1"), output, tree.MerkleRoot.Hash)This returns true. So, there you have it. A fully functional Merkle Tree implementation with proof and verification.
Conclusion
So today we implemented what we talked about last week, Merkle Trees. In our implementation we referred to RFC6962 for guidance, added a Merkle Proof method that returns the list of hashes needed to reconstruct the Merkle Tree, and added a verification method that verifies whether the proof is correct.
If you liked what you read please like, comment, and share. I’m always looking for feedback and topic suggestions.
Once again, thanks all for subscribing and tuning in this week. I will see y’all next week.
Thanks,
Ali